
- Autora Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:34.
- Última modificació 2025-01-22 16:56.
Un de primer ordre equació diferencial és exacte si té una quantitat conservada. Per exemple, equacions separables són sempre exacte , ja que per definició són de la forma: M(y)y + N(t)=0, per tant ϕ(t, y) = A(y) + B(t) és una magnitud conservada.
A més, és separable una equació diferencial?
Equacions separables . Un primer encàrrec equació diferencial y'=f(x, y) s'anomena a equació separable si la funció f(x, y) es pot factoritzar en el producte de dues funcions de x i y: f(x, y)=p(x)h(y), on p(x) i h(y) són funcions contínues.
A més, com integreu dy dx xy? Pas 1 Separeu les variables movent tots els termes y a un costat de l'equació i tots els termes x a l'altre costat:
- Multiplica els dos costats per dx:dy = (1/y) dx. Multiplica els dos costats per y: y dy = dx.
- Posa el signe integral al davant:∫ y dy = ∫ dx. Integra cada costat: (y2)/2 = x + C.
- Multiplica els dos costats per 2: y2 = 2(x + C)
D'aquesta manera, quan una equació diferencial és exacta?
El donat l'equació és exacta perquè les derivades parcials són les mateixes: ∂Q∂x=∂∂x(x2+3y2)=2x, ∂P∂y=∂∂y(2xy)=2x.
Què significa dy dx?
Per d/dx entenem que hi ha una funció a diferenciar; d/dx d'alguna cosa significa que "alguna cosa" s'ha de diferenciar respecte a x. dy/dx significa "diferenciar y respecte a x" com dy/dx significa el mateix que d/dx(y).
Recomanat:
Les xifres ocultes de pel·lícules són històricament exactes?

Exactitud històrica. La pel·lícula, ambientada al Centre de Recerca Langley de la NASA l'any 1961, mostra instal·lacions segregades com la unitat d'Informàtica de l'Àrea Oest, on originalment un grup de dones matemàtiques de color negre havia d'utilitzar menjadors i banys separats
Quines són les tres característiques que tenen en comú totes les cèl·lules?
Totes les cèl·lules dels éssers vius tenen tres coses comunes: el citoplasma, l'ADN i una membrana plasmàtica. Cada cèl·lula conté una matriu a base d'aigua coneguda com citoplasma i una membrana cel·lular selectivament permeable. Totes les cèl·lules estan formades per ADN encara que no tinguin nucli
Quines són les 4 similituds que comparteixen totes les cèl·lules?

Totes les cèl·lules tenen similituds estructurals i funcionals. Les estructures que comparteixen totes les cèl·lules inclouen una membrana cel·lular, un citosol aquós, ribosomes i material genètic (ADN). Totes les cèl·lules estan formades pels mateixos quatre tipus de molècules orgàniques: hidrats de carboni, lípids, àcids nucleics i proteïnes
Quines són totes les fórmules per a les matemàtiques?

Llista de fórmules matemàtiques Àrees. Quadrat. Volums "A=l^2". Cub. `V=s^3` Funcions i equacions. Directament proporcional. `y = kx` `k = y/x` Exponents. Producte. `a^mxxa^n=a^(m+n)` Radicals. Multiplicació. `arrel(n)(x)xxarrel(n)(y)=arrel(n)(x xx y)` Trigonometria. Ratios de trigonometria. Geometria. Fórmula polièdrica d'Euler. Vectors. Notació
Quines de les següents són totes les propietats físiques de la matèria?
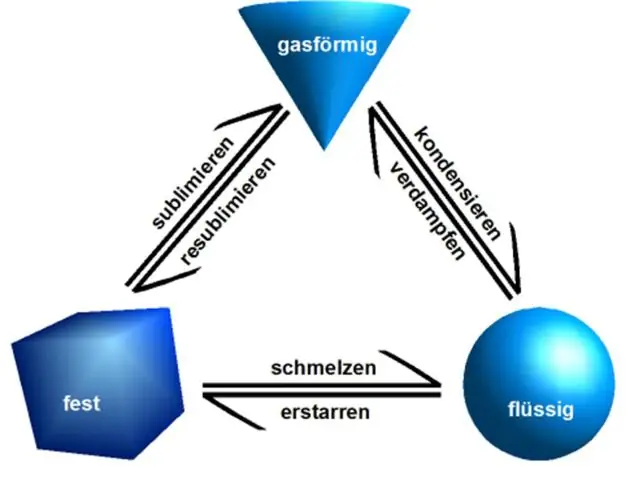
Propietats físiques: les propietats físiques es poden observar o mesurar sense canviar la composició de la matèria. Les propietats físiques inclouen: aspecte, textura, color, olor, punt de fusió, punt d'ebullició, densitat, solubilitat, polaritat i molts altres
